Pekka Buttler, June 2021 (updated October 2021 to include references to astigmatism)
Introduction
Field curvature is a term used to refer to that the ‘field’ in which a lens is focused is not level, but is instead curved. Field curvature can simultaneously be one of the most difficult design flaws to adequately deal with, while also often being real-world -irrelevant. Please, read on.
This article is part of a JAPB series of articles on the optical flaws of lenses and you can find the index of the series here.
Before we go on, I must apologize: Field curvature is a difficult topic to get one’s head around, exacerbated by the existence of a lot of less informed (but nevertheless vocal) opinions on the Interweb. I will therefore have to start by trying to go through some basics:
The basic principles:
What is ‘focus’.
One by-product of using lenses to gather more light than a pinhole camera would, is that lenses are sharp at one distance and not-sharp at other distances 1. To make a sharp image, one would either have to stop down the lens (or manufacture a naturally stopped-down lens 2), or have some contraption to allow the adjusting of at what distance the lens should be sharp. This is why most photographic lenses 3 have a focus ring or auto focus (or both).

(Right click and open in new tab for larger version)
Notice the relationship between areas that are in focus, areas that are somewhat in focus (you can discern what was there), and areas that are quite definitely out of focus
Whether you are using autofocus, a split-screen, microprisms, focus peaking, or just Mk I eyeball to ascertain focus, you’re typically selecting one point within your entire frame that you want to be in focus. Maybe it’s the blue hot-air-balloon that acts as a counterpoint to the golden sunset vista, maybe it’s the near eye of the model you’re photographing, but in general, when you focus, you’re focusing (both literally and figuratively) on one point in the frame (whether you then want the rest of the frame to be in or out of focus depends largely on your photography).
‘Field of focus’ ?
But while you’re focusing on that one point, there are all the other points to consider. Each of those other points (and your high-end camera probably has tens of megapixels, i.e. tens of millions of ‘other points’) also have a lens setting that brings them into optimum focus, and what that setting is, is dependent not only on the object’s distance from the camera, but also on the shape of the field of focus your lens produces. At any setting of the lens’ focus ring, and for every point in the frame, there is a distance from the film/sensor plane that is in optimum focus. All those points together, when mapped into 3D space, constitute the lens’ field of focus for that focusing distance.

An illustration of a lens’ field of focus being constrained to a specific distance from the focal plane (Only resized).
(Right click and open in new tab for larger version)
Field curvature: a non-flat field of focus
To understand the concept of ‘field curvature’ it is crucial to grasp that a lens’ field of focus need not be flat. Think of it like this:
• Close one eye and take a sheet of glass and hold it up so that the sheet is perpendicular (at right angles) to your eye’s optical axis. This is what a flat field of focus would look like.
• But IRL lenses’ fields of focus need not be flat. Replace that sheet of glass with a glass bowl. If you turn the bowl’s bottom toward your eye, you have a field that is curved outward; if you turn the bowl so that you’re looking into it, you have a field of focus that is curved inward.
• Depending on how deep/flat your bowl is, you are simulating different degrees of field curvature.
• Beside simply curved fields, some lenses have field curvatures that (going from the image centre towards a corner) first turn one way, then reverse. Such field curvatures are called wavy.
• The field curvature produced by a lens need not be uniform. Instead, a zoom lens’ field curvature may change as you zoom, and a prime’s field curvature may be different at infinity and MFD.
I know that understanding field curvature is difficult, even counter-intuitive. Let me try to illustrate field curvature a bit (Because I do not have the skill to make 3D visualisations of this, you’ll have to make do with some of my shoddy 2D illustrations):
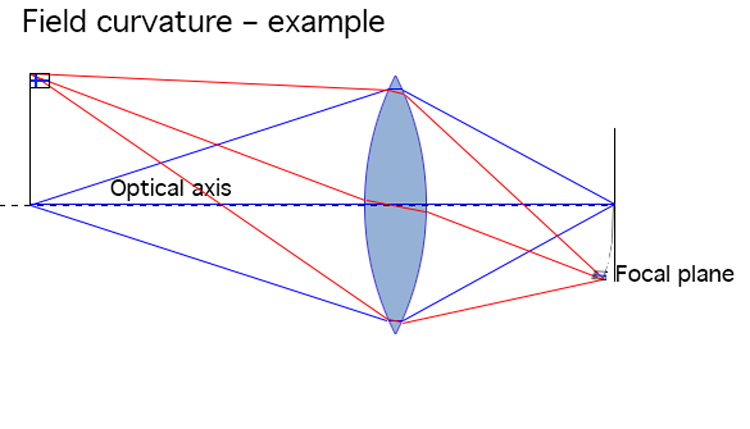
As a result, the base of the flagpole is sharp, but the top and flag are blurry and seem like they’re out of focus (because, in effect, they are).
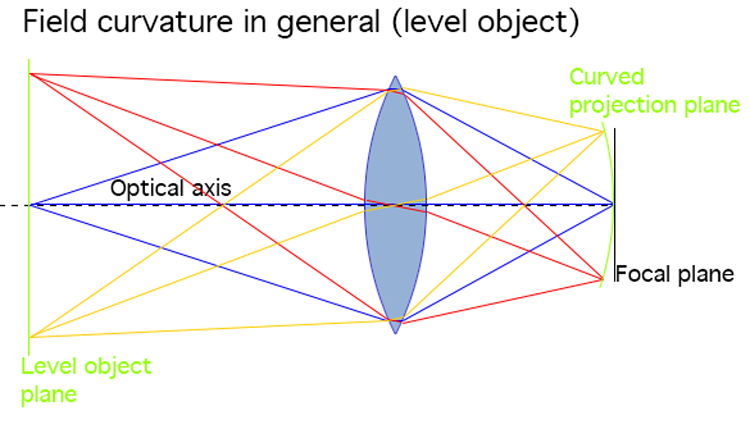
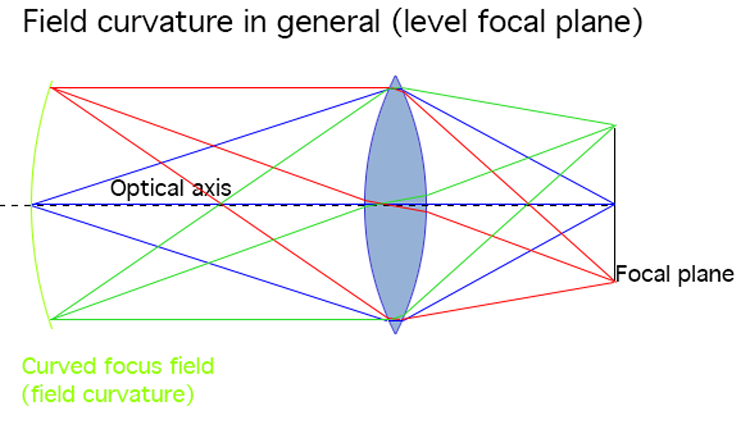
As becomes evident from these illustrations, field curvature can be summed up as: When the focal plane and object plane are not straight and parallel, then the lens has field curvature.
Why would a field of focus not be flat?
Field curvature has plagued photographers and lens designers since the dawn of photography. The long history of lens designers’ battle against field curvature can be illustrated by that Austrian-Hungarian mathematician Josef Petzval figured out the formula for field curvature (referred to as the ‘Petzval sum’) as early as 1843.
I’ll spare you the maths (I barely understand it myself), but the gist is that:
– every non-flat air-glass interface (lens surface) has an either positive or negative value
– these values are determined by a combination of the difference in refractive indices (glass/air; air/glass; glass/glass)) and the radius of the lens element’s curvature
– these values (positive and negative) are summed together and form the Petzval Sum
– for the Petzval surface to lose its curvature (i.e. become flat), the Petzval sum needs to be as close to 0 as possible (a.k.a fulfil the ‘Petzval condition’).
As almost 4 every air-glass interface either adds to or subtracts from the Petzval sum, the trick is to
a) design a lens where the the effects of all the air-glass interfaces cancel each other out, while still
b) designing a lens that manages to bend light in a way that is suitable for the lens’ intended use 5.
Of these, that latter point is the real kicker, because to be able to do its magic, a lens may need to use various aggressively shaped lens elements with significant refractive indices. Even so, a lens designer’s task to compute a lens with little to no actual field curvature is made harder whenever:
– one cannot use a perfectly or nearly symmetric lens design
– the lens’ field-of-view is significantly divergent from the so called standard lens (ultrawides and superteles are the hardest)…
– we’re talking about a zoom lens, even worse if it has a significant zoom ratio.
– the lens is supposed to be very bright (large maximum aperture)…
– special glass compounds are not available or prohibitively expensive considering the customer segment.
As a result of this, a significant share of lenses evidence such a level of field curvature that you can detect it in the field (i.e. without a lab).
The field-relevance of field curvature
Again, because a lot of pundits decry all lenses that show any field curvature as useless abominations, I feel the need to address the question of whether (or: when) field curvature actually is a problem.
As stated above: field curvature means, that the focal plane (film/sensor) and the object plane are not perfectly flat and parallel. Given that all films and sensors are flat, field curvature is a critical issue when we’re using lenses on straight and level surfaces.
There are a number of scenarios where field curvature therefore needs to be very near to non-existent:
• enlarger lenses exist to project the image of a (level) negative onto a level paper
• projection lenses project the image of a (level) slide onto a (level) wall or screen
• reproduction lenses exist to take perfect copies of (level) objects such as documents or slides
• photolithography …
But unless you’re in the practice of photographing perfectly flat planes such as the above (or brick wall shots, or test charts), you’re mostly dealing with sceneries where some objects are ‘behind’ your intended point of focus, and some might even be ‘in front’ of your point of focus. In such situations you will either have to accept that your entire scene is not in focus, or significantly stop down your lens to get everything in focus.
This raises two further, important aspects: wide-open softness and depth-of field.
While we’ve recently seen a number of groundbreaking lenses that are so superbly corrected (and huge and heavy) that they suffer field-negligible wide-open softness, a vast majority of all lenses ever made suffer from being decidedly less sharp (having less definition and contrast) when used wide open. The main causes of this effect are spherical aberration, astigmatism, coma and longitundinal chromatic aberration. But – when doing real photography – depth-of-field is crucially important.
Depth-of-field
When you’ve focused a lens (to any distance), there is always a distance at which (distance) focus is optimal. Theoretically, that field of optimum focus is always razor-thin, but in practice we’ve taken to accept that this field has a thickness – a range of distances where focus is acceptable. That thickness is the depth-of-field 6.
The depth-of-field (or thickness of the field of focus) is a physical (unavoidable) function of how lenses work. In principle, the depth of field decreases (becomes thinner, shallower) when subject/focusing distance gets shorter; when focal length increases; and when the aperture gets larger.
Assuming focal length and focusing distance are unchanged, the aperture’s effect on depth of field is reflected by the table below:
| Aperture | Depth-of-field |
| f/1.4 | 1,02 cm |
| f/2 | 1,46 cm |
| f/2.8 | 2,06 cm |
| f/4 | 2,92 cm |
| f/5.6 | 4,13 cm |
| f/8 | 5,85 cm |
| f/11 | 8,29 cm |
| f/16 | 11,8 cm |
| f/22 | 16,8 cm |
Assuming you’re taking a portrait of a model or family member, depth of field is the reason why when you focus on a model’s near eye, other parts of the face and head are liable to be visibly out of focus.

Revuenon MC 50 mm f/1.4 on Sony a7R2

Olympus OM Zuiko 55 mm f/1.2 @ f/1.2, 1/125 s, ISO 3200, Sony ⍺7R. Post-processed.
The interplay of field curvature and depth-of-field
Thinking back to the example mentioned above (the field of sharpness as a glass bowl), the thickness of the bowl (how thick the glass is) becomes significant. The following illustrations will hopefully explain.
To take an extreme example we’ll be doing our calculations based on a brick wall (or other level surface). The other crucial metrics are: full frame, f=85 mm, max aperture f/2, focusing distance: 1 metre.
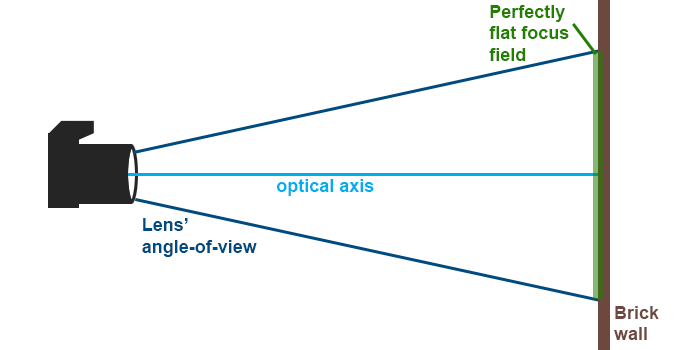
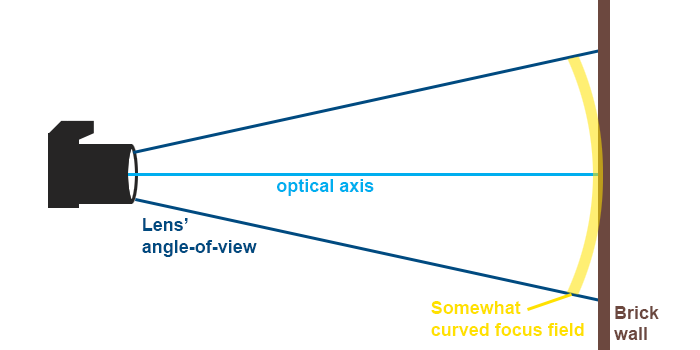
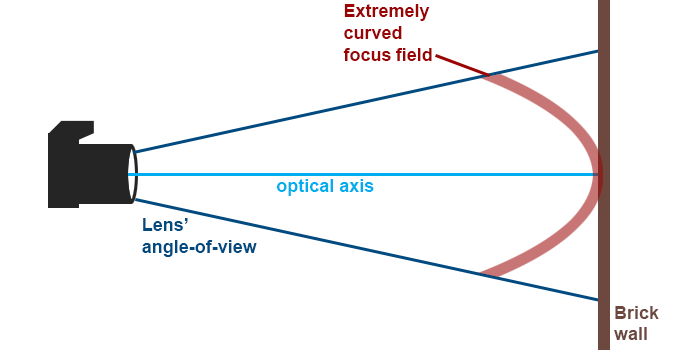
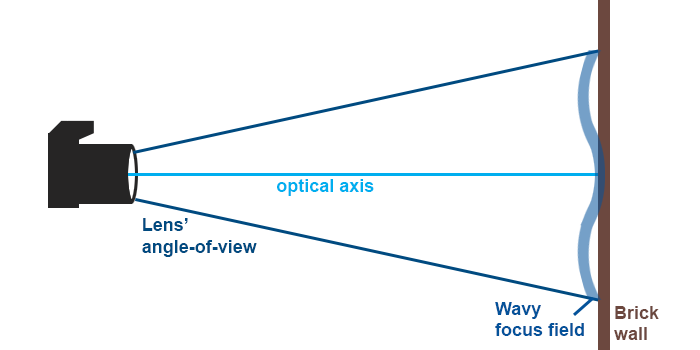
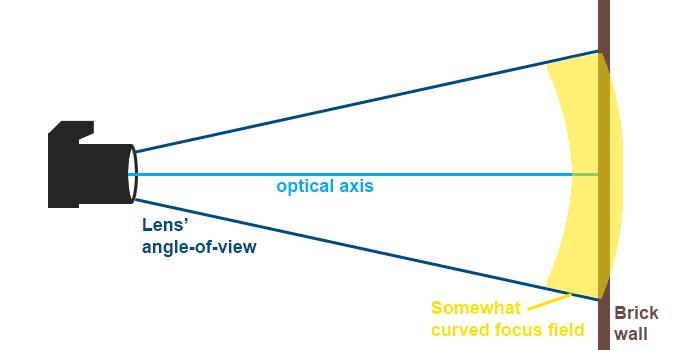
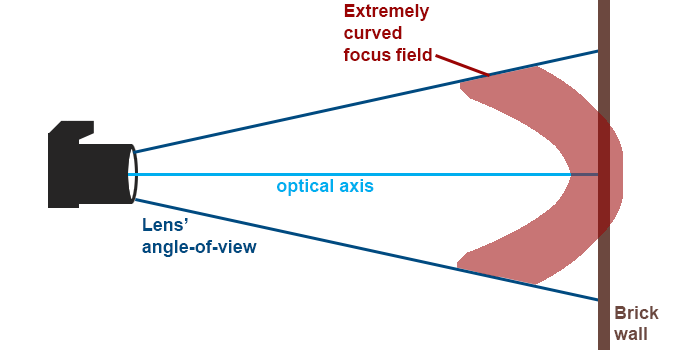
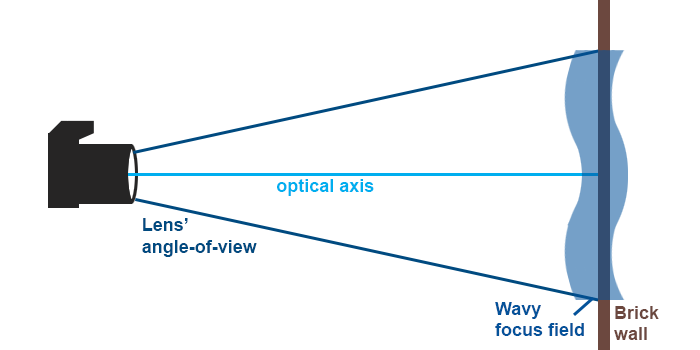
Does this lens of mine have field curvature?
Without knowing what lens you’re thinking about, I can’t answer, but a safe bet would be to say: yes. The more important question, however, is: how much?
Luckily, there’s a relatively simple test you can easily conduct. You will need:
– a camera that allows live preview (mirrorless camera or dSLR with live view) with decent live magnification,
– the lens you intend to put to the test,
– a tripod,
– a perfectly flat, textured surface (Brick walls work, but if you want to do this at home, fasten some newspapers onto the wall), and
– some way to make sure your optical axis is at a 90º angle to your object.
Of these, that last one might be liable to be the biggest ‘waitamoment’, but if you’re inventive, you’ll use anything from a piece of furniture to a sheet of paper to make sure you’re working at right angles (your camera’s artificial horizon may give you the y-axis, but for the x-axis some gimmicry might be needed)
Testing procedure
Work through this regime, starting at wide open and, going to medium apertures (f/5.6-f/11 depending on lens)
1) Set lens to desired aperture
2) using live preview at maximum magnification and adjust the lens’ focus for an optimal centre focus
3) Note the setting of the focus ring (take a picture with your smartphone)
4) using live preview at maximum magnification and adjust the lens’ focus for a mid-zone focus.
5) Note the setting of the focus ring (take a picture with your smartphone)
6) using live preview at maximum magnification and adjust the lens’ focus for a extreme corner focus 7.
7) Note the setting of the focus ring (take a picture with your smartphone)
Note: You can also take photographs at stages 3, 5, and 7. Also, you may want to skip the mid-zone focus part (steps 4 &5).
Data analysis
Analysis of focus ring position:
(a= centre focus; b= mid-zone focus; c= extreme corner focus)
– If a=b=c, you have a remarkably flat focus field
– if a<b<c, you have a concave (edges turned toward the camera) field.
– if a>b>c, you have a convex (edges turned away from the camera) field.
– if a<b>c or a>b<c, you have a wavy field curvature
The difference between a&b / b&c defines whether field curvature is mild or wild.
Analysis of images
(P1=image focused on centre; P2=image focused on mid-zone; P3=image focused on corner;
CF=centre focus; MZF= mid-zone focus; CF=corner focus)
For each shot, isolate all the parts of the image you focused on.
– If CF on P1, P2, and P3 are equally good. you have a remarkably flat focus field
– If CF on P1 is better than on P2, which is better than on P3, you have field curvature (convex or concave – cannot say)
– If CF is better on P1 than on P2, but is also better on P3 then on P2, then you have wavy field curvature
– you have bad field curvature if CF on P2 or P3 is not only ‘not quite as good’ as on P1, but is actually bad.
Rant
For more than one hundred years, the photographic industry has largely accepted the notion, that a ‘good’ lens will have a flat field of sharpness that runs parallel to the film/sensor plane 8. Granted, there are a number of situations (enumerated above) in which it is obvious that the focal plane and film/sensor plane must run absolutely parallel, those are not general photography situations and those lenses are not offered for general photography purposes.
Genuine general photography is characterised by having objects in the frame that are at different distances. Consider, that the current obsession with narrow depth-of-field to allow the isolating of subject from background is – above all else – a testament to that photography is not photolithography. Even so, the ubiquitous practice of doing sharpness tests by shooting flat targets (test cards or brick walls) relies on the assumption that ‘flat focal plane = as it should be’.
But as anyone who’ll know a bit about lens design can tell you:
• very few lenses have a naturally perfectly flat field (especially not SLR lenses with the longish back focus distance demanded by the mirror box)…
• many lenses are designed to sacrifice a flat field of focus (or, they used to be until this ‘wide open corner sharpness’ craze hit) in order to either achieve another worthwhile goal, because lens design is always a business of trade-offs and compromises.
• there are cases where you’d want to have field curvature. For instance, a strongly concave field curvature helps increase subject separation between a central foreground subject and a background, and the interaction of field curvature with other aberrations is what gives the Helios 44 (and a number of other lenses) their signature swirl effect.
• Some lenses have even implemented systems to allow the photographer to tweak field curvature (e.g. the Minolta 24 mm VFC).
On the other hand, there are certainly situations where field curvature can render a lens unsuitable for general purpose photography. Take, for example, a lens that has a field that in the corners is severely curved away from the camera. While it could certainly be used for some things (e.g. studio and product photography), you could never use it for landscape photography (never mind astrophotography), because if you focus on the horizon in the centre, it would in the corners be focused far beyond infinity.
But there is a middle ground: lenses that have a share of field curvature (that will forever ruin that lens’ chances in modern sharpness-crazed reviews), but will – in real life photography – be totally usable.
So just because your lens’ design has field curvature as a byproduct, don’t despair. Analyse the lens, and get to know its profile, and maybe you’ll find a way to use its flaws to your advantage.
P.S.
For the sake of keeping things even mildly simple, I’ve omitted one central element from this entire discussion of field curvature. Namely, I’ve pretended that there is only one field of focus, while – in fact – there are (once we progress a bit away from the optical axis) three: One plane (the Petzval surface) that defines the theoretical optimal focus, one that defines the optimal sagittal focus (for off-axis light), and one that defines the optimal tangential focus (for off-axis light). While – in a lens designer’s wet dream – these three planes can be made to coincide perfectly, most often they do not. When they do not, the lens suffers from astigmatism (but that’s another story for another article)
Footnotes
1 Pinhole-camera photographs’ sharpness is limited by a combination of the pinhole’s size and diffraction, but one aspect of pinhole cameras is that the images are sharp (or as sharp as the design allows) all the way from close objects to infinity.
2 Many simple cameras from the bygone era used relatively dim lenses that either could not be focused at all (e.g. Kodak Brownies, many Agfamatic’s) or which allowed setting focus only for 2–3 zones, e.g. portrait, group shot, landscape (e.g. Agfa Optima 1).
3 The exception to this rule is based on enlarger lenses (that were focused using a bellows) and some macro lenses meant to be used with a dedicated bellows.
4 With the exception of flat lens surfaces.
5 Josef Petzval is (today) more known for an (at the time (1840)) revolutionary design for a fast portrait lens, often referred to as a Petzval lens. Ironically, Petzval lenses suffer significant field curvature (have a high Petzval sum). See more here. On the other hand, in their intended use (portraiture) field curvature can be an asset.
6 The customary concept of depth-of-field is based on the idea of ‘viewing distance’. In other words, that for each size of print, there is a minimum viewing distance: The bigger the print, the farther away you will be when looking at it, the less your (average) eyes will be able to discern detail. In this approach, the amount of pixels that make up the image (and the physical size of those pixels) are irrelevant.
If, however, you’re in the custom of pixel-peeping (studying images on your screen in 1:1 zoom), you are – in effect – circumventing the concept of viewing distance, and objects that are comfortably within the depth of field will start to look like they’re out of focus.
Therefore, the customary concept and measurements of depth-of-field do not hold for pixel-peeping.
7 I recommend selecting one corner and sticking with it, to be able to differentiate between field curvature and decentering,
8 This has even gone as far as that some cameras have implemented contraptions to change the shape of the film plane in order to compensate for the lens’ lack of ability to project a level and parallel focal plane.
Read more:
Note, please: There are many sources for data on Field curvature. Sadly, many of them are liable to give you an erroneous impression. The following links are – while not always complete and not always entirely correct – among the better popular sources I’ve managed to find.
Field curvature on MicroscopyU
Field curvature on Discover Digital Photography
Field curvature on Photographylife
Field curvature illustrations on Lens Rentals
Discussion of lens designs and their pros and cons on PencilOfRays.com
Petzval Sum on OptoWiki